Seepage

For the music album, see Seepage (EP).

A cross section showing the water table varying with surface topography as well as a perched water table

In soil mechanics, seepage is the movement of water through soil. If fluid pressures in a soil deposit are uniformly increasing with depth according to $u=\rho _{w}gz_{w}$, where $z_{w}$ is the depth below the water table, then hydrostatic conditions will prevail and the fluids will not be flowing through the soil. However, if the water table is sloping or there is a perched water table as indicated in the accompanying sketch, then seepage will occur. For steady state seepage, the seepage velocities are not varying with time. If the water tables are changing levels with time, or if the soil is in the process of consolidation, then steady state conditions do not apply.

Darcy's law

Diagram showing definitions and directions for Darcy's law

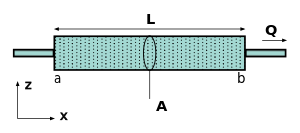
Darcy's law states that the volume of flow of the pore fluid through a porous medium per unit time is proportional to the rate of change of excess fluid pressure with distance. The constant of proportionality includes the viscosity of the fluid and the intrinsic permeability of the soil. For the simple case of a horizontal tube filled with soil

$Q={\frac {-KA}{\mu }}{\frac {(u_{b}-u_{a})}{L}}$

The total discharge, $Q$ (having units of volume per time, e.g., ft³/s or m³/s), is proportional to the intrinsic permeability, $K$, the cross sectional area, $A$, and rate of pore pressure change with distance, ${\frac {u_{b}-u_{a}}{L}}$, and inversely proportional to the dynamic viscosity of the fluid, $\mu$. The negative sign is needed because fluids flow from high pressure to low pressure. So if the change in pressure is negative (in the $x$-direction) then the flow will be positive (in the $x$-direction). The above equation works well for a horizontal tube, but if the tube was inclined so that point b was a different elevation than point a, the equation would not work. The effect of elevation is accounted for by replacing the pore pressure by excess pore pressure, $u_{e}$ defined as:

$u_{e}=u-\rho _{w}gz$

where $z$ is the depth measured from an arbitrary elevation reference (datum). Replacing $u$ by $u_{e}$ we obtain a more general equation for flow:

$Q={\frac {-KA}{\mu }}{\frac {(u_{e,b}-u_{e,a})}{L}}$

Dividing both sides of the equation by $A$, and expressing the rate of change of excess pore pressure as a derivative, we obtain a more general equation for the apparent velocity in the x-direction:

$v_{x}={\frac {-K}{\mu }}{\frac {du_{e}}{dx}}$

where $v_{x}=Q/A$ has units of velocity and is called the Darcy velocity (or the specific discharge, filtration velocity, or superficial velocity). The pore or interstitial velocity $v_{px}$ is the average velocity of fluid molecules in the pores; it is related to the Darcy velocity and the porosity $n$ through the Dupuit-Forchheimer relationship

$v_{px}={\frac {v_{x}}{n}}$

(Some authors use the term seepage velocity to mean the Darcy velocity, while others use it to mean the pore velocity.)

Civil engineers predominantly work on problems that involve water and predominantly work on problems on earth (in earth's gravity). For this class of problems, civil engineers will often write Darcy's law in a much simpler form:

$v=ki$

where $k$ is the hydraulic conductivity, defined as $k={\frac {K\rho _{w}g}{\mu _{w}}}$, and $i$ is the hydraulic gradient. The hydraulic gradient is the rate of change of total head with distance. The total head, $h$ at a point is defined as the height (measured relative to the datum) to which water would rise in a piezometer at that point. The total head is related to the excess water pressure by:

$u_{e}=\rho _{w}gh+Constant$

and the $Constant$ is zero if the datum for head measurement is chosen at the same elevation as the origin for the depth, z used to calculate $u_{e}$.

Typical values of hydraulic conductivity

Values of hydraulic conductivity, $k$, can vary by many orders of magnitude depending on the soil type. Clays may have hydraulic conductivity as small as about $10^{-12}{\frac {m}{s}}$, gravels may have hydraulic conductivity up to about $10^{-1}{\frac {m}{s}}$. Layering and heterogeneity and disturbance during the sampling and testing process make the accurate measurement of soil hydraulic conductivity a very difficult problem.

Flownets

Main article: Flownet

A plan flow net to estimate flow of water from a stream to a discharging well

Darcy's Law applies in one, two or three dimensions. In two or three dimensions, steady state seepage is described by Laplace's equation. Computer programs are available to solve this equation. But traditionally two-dimensional seepage problems were solved using a graphical procedure known as flownet. One set of lines in the flownet are in the direction of the water flow (flow lines), and the other set of lines are in the direction of constant total head (equipotential lines). Flownets may be used to estimate the quantity of seepage under dams and sheet piling.

Forces and erosion

When the seepage velocity is great enough, erosion can occur because of the frictional drag exerted on the soil particles. Vertically upwards seepage is a source of danger on the downstream side of sheet piling and beneath the toe of a dam or levee. Erosion of the soil, known as "soil piping", can lead to failure of the structure and to sinkhole formation. Seeping water removes soil, starting from the exit point of the seepage, and erosion advances upgradient. The term "sand boil" is used to describe the appearance of the discharging end of an active soil pipe.

Pressures

Seepage in an upward direction reduces the effective stress within the soil. When the water pressure at a point in the soil is equal to the total vertical stress at that point, the effective stress is zero and the soil has no frictional resistance to deformation. For a surface layer, the vertical effective stress becomes zero within the layer when the upward hydraulic gradient is equal to the critical gradient. At zero effective stress soil has very little strength and layers of relatively impermeable soil may heave up due to the underlying water pressures. The loss in strength due to upward seepage is a common contributor to levee failures. The condition of zero effective stress associated with upward seepage is also called liquefaction, quicksand, or a boiling condition. Quicksand was so named because the soil particles move around and appear to be 'alive' (the biblical meaning of 'quick' – as opposed to 'dead'). (Note that it is not possible to be 'sucked down' into quicksand. On the contrary, you would float with about half your body out of the water.)